Search
Duplicate
🖋️

어떤 추천시스템을 사용해야 할까? (1) - 협업 필터링 모델과 한계점

Created
2022/07/30
Editor
목차

1. 추천 시스템: 콘텐츠 기반 필터링 모델과 협업 필터링 모델

추천 시스템에는 대표적으로 두가지 모델이 있습니다.
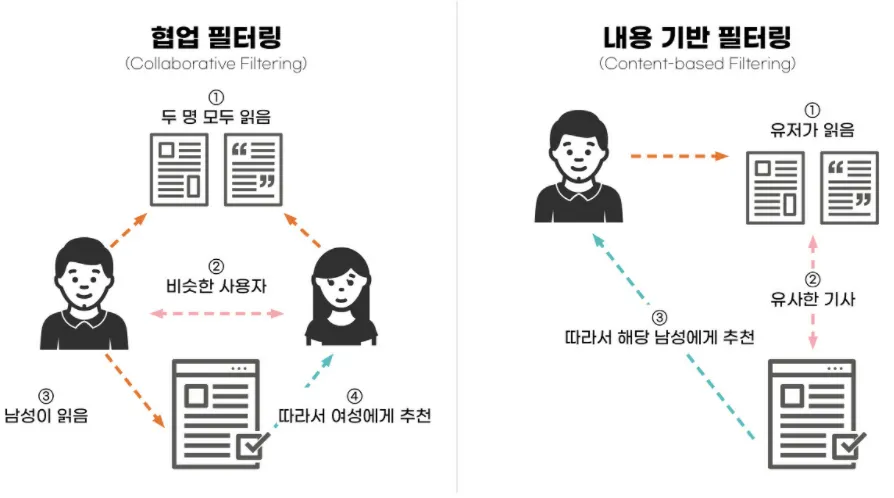
첫번째는 콘텐츠 기반 필터링 모델(Content-based Filtering)은 콘텐츠만을 활용하여 추천해주는 알고리즘인데요, 사용자가 좋아하는 콘텐츠를 분석하여 그와 유사한 콘텐츠를 추천해주는 기술입니다. 예를 들어 사용자가 “All I want for Christmas is you”라는 노래를 감상했다면, 이를 바탕으로 겨울과 관련된 노래를 추천해줄 수 있습니다.
두번째는 협업 필터링 모델(Collaborative Filtering, CF)인데요, 이것은 다른 사용자들로부터 취향 정보들을 모아 사용자의 관심사를 예측하는 방법입니다. CF 모델은 비슷한 취향을 가진 사용자들은 어떠한 아이템에 대해 비슷한 선호도를 가질 것이라는 가정 하에 사용자와 아이템 간 상호 작용 데이터를 활용합니다. 만약 캐롤을 좋아하는 사람들이 공통적으로 판타지 영화에 대해 높은 선호도를 보인다면 사용자에게 “해리포터”를 추천해줄 수도 있겠죠.
출처: 마음을 읽는 개인화 마케팅의 시대
콘텐츠 기반 필터링 모델과 협업 필터링 모델은 상호보완적인 역할을 합니다. 새로운 아이템이 출시된 경우 아이템을 사용한 사용자의 데이터가 없기 때문에 협업 필터링 모델을 사용하기 어렵지만 콘텐츠 기반 필터링 모델에서는 텍스트나 이미지 유사성 기반의 추천이 가능합니다.
반면 협업 필터링 모델은 사용자와 아이템 간의 상호작용을 바탕으로 하기 때문에 텍스트/이미지 기반 유사성이 높지 않더라도, 사용자가 함께 구매한 아이템을 추천합니다.
우선 이번주에는 추천 시스템에서 가장 많이 사용되는 협업 필터링 모델에 대해 알아보고, 다음주의 글에서는 협업 필터링의 한계를 보완하는 콘텐츠 기반 필터링을 소개하려고 합니다.

2. 협업 필터링 모델의 유형

협업 필터링 모델은 크게 메모리 기반 접근 방식과 모델 기반 접근 방식으로 나뉩니다.

(1) 메모리 기반 접근 방식

가장 전통적인 접근 방식이며 유사도를 기반으로 동작합니다. 사용자 간 유사도를 기준으로 하는 경우에는 사용자 기반 추천, 아이템 간 유사도를 기준으로 하는 경우에는 아이템 기반 추천이라고 합니다.
•
사용자 기반 추천 (User-based Recommendation)
사용자 기반 추천은 비슷한 성향을 지닌 사용자들을 그룹화하여, 그룹이 선호하는 상품을 해당 그룹에 속한 사용자에게 추천합니다.
예를 들어 사용자 A와 B가 비슷한 성향을 가지고 있는데, B가 아이스크림을 좋아한다면 A역시 아이스크림을 좋아할 것이라고 예측하고 관련 정보를 추천하는 방식입니다. 인스타그램 같은 SNS의 친구 추천 방식도 이와 같은데요, 나의 팔로워를 나와 비슷한 성향을 가진 사람으로 인식하고 그의 또 다른 팔로워들을 나에게 추천합니다.
•
아이템 기반 추천 (Item-based Recommendation)
아이템 기반 추천은 사용자가 이전에 구매했던 아이템을 기반으로 그 상품과 유사한 다른 상품을 추천하는 방식입니다. 상품 간 유사도는 함께 구매되는 경우의 빈도를 분석하여 측정하는데요, 예를 들어 아이스크림과 와플이 함께 구매되는 경우가 많다면 아이스크림을 구매한 사용자에게 와플을 추천하는 것입니다.

(2) 모델 기반 접근 방식

메모리 기반 접근 방식이 기존의 데이터를 이용한 추천 방식이었다면, 모델 기반 접근 방식은 기계 학습을 통해 사용자 또는 아이템의 숨겨진 특성 값을 계산하는 방식입니다. 모델 기반의 접근 방식에는 잠재요인을 이용한 Latent Factor 방식과 Classification/Regression(분류/회귀)방식 및 최신 융합 모델 방식을 이용한 다양한 접근 방식이 있습니다.
•
Latent Factor 모델
사용자와 아이템을 잠재적인 차원(Factor)들을 사용해 나타낼 수 있다고 가정하는 모델입니다.
여기서의 차원은 축(axis)과 같은 의미로 사용되는데요, 예를 들어 x축에는 성별을 나타내고 y축에는 영화의 장르를 나타내는 좌표평면이 있다면, 사용자와 아이템은 좌표평면 위의 적절한 x, y 값에 매핑된다는 것입니다. 사용자 = (-2.5, -3.2), 영화 = (1.5, 4.6) 처럼 말이죠. 이 예시에서는 사용자와 아이템을 x축과 y축의 두 가지 차원으로 표현했지만 실제 Latent Factor 방식에서는 차원이 무엇을 의미하는지 알 수 없으며, 차원의 개수 또한 여러개일 수 있습니다. 그렇기 때문에, 사용자와 아이템의 매핑 지점이 가까울수록 유사하다고 판단합니다.
•
Classification/Regression 방식(분류/회귀)
Classification/Regression 방식은 콘텐츠 기반 추천 방식과 쉽게 융합이 가능합니다. 피처 X 가 주어졌을 때, 라벨 y를 예측하는 구조이기 때문에, 피드백 y를 예측하는 상황에서,  X에 콘텐츠 관련 정보를 피처로 만들어서 추가하면, 피드백 데이터뿐만 아니라 콘텐츠 데이터를 활용한 추천이 가능합니다.
구체적으로 Classification은 유저의 성향에 따라 군집을 분류하여 성향이 부여된 군집에 맞추어 아이템을 추천해 주는 방식이고, Regression은 유저와 아이템에 대한 평균 평점을 구하는 모델을 통해 새로운 카테고리에서 예측값을 예측하여 추천하는 방식입니다.
•
최신 융합 모델 방식
최근에는 Latent Factor 모델과 Classification/Regression 모델의 특징을 모두 가진 Factorization Machine, 딥러닝을 활용하여 Latent Factor 모델을 확장한 Neural Collaborative Filtering도 제시되었습니다.

3. 협업 필터링 모델의 알고리즘

(1) 메모리 기반 접근 방식

위에서 모델의 유형을 설명 할 때 메모리 기반 접근 방식은 유사도를 측정하여 사용한다고 했는데요. 이 때 두 사용자 간의 유사도는 두 벡터 간의 유사도로 정의할 수 있습니다. 두 벡터 간 유사도를 구하기 위해서 일반적으로 코사인 유사도(Cosine Similarity)와 피어슨 유사도(Pearson Similarity)입니다.
•
코사인 유사도
코사인 유사도는 두 벡터의 코사인 각도를 계산하여 유사성을 측정합니다. 코사인 함수를 생각해 보면 0도에서의 값이 1, 180도에서의 값이 -1이죠. 두 벡터가 서로 가까우면 각도가 작아서 값이 1에 가까워져 유사하다고 하고, 두 벡터가 서로 대척되면 각도가 커져서 값이 -1에 가까워져 유사하지 않다고 하는 것입니다. 이를 직관적으로 이해하면 두 벡터가 가리키는 방향이 얼마나 유사한가를 의미합니다.
◦
사용자 uu와 사용자 vv간의 코사인 유사도
cosine_sim(u,v)=∑i∈Iuvr(u,i) ⋅ r(v,i)∑i∈Iuvr(u,i)2 ⋅ ∑i∈Iuvr(v,i)2\rm{cosine\_sim(u,v)} = \frac {{\sum_{i \in I_{uv}} r(u,i)\ · \ r(v,i)}}{\sqrt {\sum_{i \in I_{uv}} r(u,i)^2} \ · \ \sqrt {\sum_{i \in I_{uv}} r(v,i)^2}}
◦
상품 ii와 상품 jj간의 코사인 유사도
cosine_sim(i,j)=∑u∈Uijr(u,i) ⋅ r(u,j)∑u∈Uijr(u,i)2 ⋅ ∑u∈Uijr(u,j)2\rm{cosine\_sim(i,j)} = \frac {{\sum_{u \in U_{ij}} r(u,i)\ · \ r(u,j)}}{\sqrt {\sum_{u \in U_{ij}} r(u,i)^2} \ · \ \sqrt {\sum_{u \in U_{ij}} r(u,j)^2}}
•
피어슨 유사도
피어슨 유사도(Pearson Similarity)는 두 벡터의 상관계수(Pearson correlation coefficient)를 말하며 다음과 같이 정의합니다.
◦
사용자 uu와 사용자 vv간의 피어슨 유사도
pearson_sim(u,v)=∑i∈Iuv(r(u,i) − μ(u)) ⋅ (r(v,i) − μ(v))∑i∈Iuv(r(u,i) − μ(u))2 ⋅ ∑i∈Iuv(r(v,i) − μ(v))2\rm{pearson\_sim(u,v)} = \frac {{\sum_{i \in I_{uv}} (r(u,i) \ - \ \mu(u))\ · \ (r(v,i) \ - \ \mu(v))}}{\sqrt {\sum_{i \in I_{uv}} (r(u,i) \ - \ \mu(u))^2} \ · \ \sqrt {\sum_{i \in I_{uv}} (r(v,i) \ - \ \mu(v))^2}}
◦
상품 ii와 상품 jj간의 피어슨 유사도
pearson_sim(i,j)=∑u∈Uij(r(u,i) − μ(i)) ⋅ (r(u,j) − μ(j))∑u∈Uij(r(u,i) − μ(i))2 ⋅ ∑u∈Uij(r(u,j) − μ(j))2\rm{pearson\_sim(i,j)} = \frac {{\sum_{u \in U_{ij}} (r(u,i) \ - \ \mu(i))\ · \ (r(u,j)\ - \ \mu(j))}}{\sqrt {\sum_{u \in U_{ij}} (r(u,i)\ - \ \mu(i))^2} \ · \ \sqrt {\sum_{u \in U_{ij}} (r(u,j)\ - \ \mu(j))^2}}
계산된 피어슨 유사도가 1이면 양의 상관관계(비교하는 데이터 중 하나가 증가하면 다른 하나도 증가함), -1이면 음의 상관관계(하나가 증가하면 다른 하나는 감소함), 0이면 상관관계가 없음(독립)을 의미합니다.
그럼 간단한 예시 상황을 가정하여 유사도를 구해보도록 하겠습니다. 아래의 표는 사용자들이 영화 평점을 0~5점 사이의 값으로 표현한 결과 표입니다. 빈칸은 평가하지 않은 항목입니다.
기생충
겨울왕국
스파이더맨
라라랜드
미나리
A
5
4
4
3
B
1
0
1
4
C
4
4
5
3
D
2
1
4
3
E
4
4
4
2
F
4
2
3
1
코사인 유사도를 이용해 B와 D의 유사도를 구해보겠습니다. 유사도를 구할 때에는 두 사용자가 공통으로 평가한 항목(겨울왕국, 스파이더맨, 미나리)에 대해서만 계산하기 때문에, u=(0, 1, 4), v=(2, 1, 3)으로 두고 계산하면 유사도는 다음과 같습니다.
similarity = (0,1,4) ⋅ (2,1,3)02+12+42 × 22+12+32 = 1317 × 14 ≅ 0.84similarity \ = \ \frac{(0,1,4)\ \cdot \ (2,1,3)}{\sqrt{0^2+1^2+4^2} \ \times \ \sqrt{2^2+1^2+3^2}} \ = \ \frac{13}{\sqrt{17} \ \times \ \sqrt{14}} \ \cong \ 0.84
이러한 방법으로 모든 사용자에 대해서 유사도를 구하면 아래와 같이 나오는데요.
similarity
A
B
C
D
E
F
A
1
0.84
0.96
0.82
0.98
0.98
B
0.84
1
0.61
0.84
0.63
0.47
C
0.96
0.61
1
0.97
0.99
0.92
D
0.82
0.84
0.97
1
0.85
0.71
E
0.98
0.63
0.99
0.85
1
0.98
F
0.98
0.47
0.92
0.71
0.98
1
이를 활용하여 특정 인물이 평가하지 않았던 영화에 대한 평가 점수를 예측해볼 수 있습니다. 예를 들어 가장 유사한 몇명의 점수를 이용하여 예측 점수로 구할 수도 있고, 전체를 대상으로 유사도 기반의 weighted sum 값을 예측 점수로 사용하는 거죠. E의 겨울왕국에 대한 평가 점수를 2번째 방법으로 예측해보면 다음과 같습니다.
prediction = 0.98×4+0.63×0+0.99×4+0.85×2+0.98×20.98+0.63+0.99+0.85+0.98 = 2.60prediction \ = \ \frac{0.98\times4+0.63\times0+0.99\times4+0.85\times2+0.98\times2}{0.98+0.63+0.99+0.85+0.98} \ = \ 2.60

(2) 모델 기반 접근 방식

이 방법은 머신러닝 알고리즘을 통해, 사용자가 아직 평가하지 않은 아이템의 평점을 예측합니다. 사용자의 선호도가 소수의 잠재된 요인으로 결정될 수 있다는 아이디어를 바탕으로 하기 때문에 행렬 분해를 이용하여 잠재된 요인을 추출합니다.
행렬 분해는 User-Item Matrix를 F차원의 User와 Item의 latent factor 행렬곱으로 분해하는 방법을 말합니다. User-Item Matrix의 유저 u의 아이템 i에 대한 선호도는 다음과 같이 User/Item Latent Matrix의 벡터의 곱으로 표현될 수 있습니다. 이 표현을 통해 유저가 평가하지 않은 선호도에 대해서도 아래의 수식을 통해 쉽게 추정할 수 있으며 내적 값이 높을수록 유저 u에게 아이템 i가 더 좋은 추천이라는 것을 알 수 있습니다.
rui^ = qiTpu\hat{r_{ui}} \ = \ q_i^Tp_u
•
pu, qi ∈ Rfp_u, \ q_i \ \in \ \mathbb{R^f} : User, Item Latent Matrix의 벡터
•
rui^\hat{r_{ui}} : 유저 u의 아이템 i에 대한 선호도 추정 값

4. 협업 필터링의 한계

모든 알고리즘이 그렇듯 협업 필터링에도 몇 가지 한계가 있습니다.
•
콜드 스타트(Cold start)
협업 필터링을 사용하기 위해서는 기존 데이터를 활용해야 합니다. 사용자 기반 추천방식에서는 신규 사용자의 행동이 기록되지 않으면, 어떤 아이템도 추천하지 못한다는 문제가 발생합니다. 아이템 기반 추천방식에서도, 신규 상품이 출시되더라도 이를 추천할 수 있는 정보가 쌓일 때까지 추천을 할 수 없다는 의미입니다. 즉, 시스템이 아직 충분한 정보를 모으지 못하면 사용자에 대한 추론을 이끌어 내지 못해 추천을 할 수 없는 한계가 있습니다.
•
계산 효율 저하
협업 필터링은 계산량이 많은 알고리즘이기 때문에 사용자가 많아질수록 계산 시간 증가하게 됩니다. 사용자가 많아야 정확한 추천 결과를 도출할 수 있지만, 동시에 계산 시간도 증가하기 때문에 길게는 며칠이 걸리기도 합니다. 이렇게 알고리즘의 정확도와 걸리는 시간이라는 상충되는 문제점은 협업 필터링의 딜레마입니다.
•
롱테일(Long-Tail) 문제
파레토 법칙(전체 결과의 80%가 전체 원인의 20%에서 일어나는 현상)을 그래프로 나타내었을 때 꼬리처럼 긴 부분을 형성하는 80%의 부분을 롱테일이라고 합니다. 이는 사용자들이 관심을 많이 보이는 소수의 인기 있는 콘텐츠를 주로 추천하여 ‘비대칭적 쏠림 현상'이 발생한다는 의미입니다. 사용자들은 소수의 인기 있는 항목에만 관심을 보이고 관심이 저조한 아이템은 정보가 부족하여 추천되지 못하여, 다양성이 떨어지는 문제가 발생합니다.
협업 필터링은 몇가지 단점에도 불구하고 간결함과 정확성 덕분에 아직까지도 많은 추천 시스템에서 활용되고 있습니다. 한편으로는 이러한 한계점을 극복하기 위해 콘텐츠에 대한 분석을 기반으로 추천하는 방식이 등장하게 되는데요, 영화 콘텐츠의 경우라면 감독, 장르, 등장인물 등을 분석하고, 상품이라면 상품 설명, 종류 등을 분석합니다. 그럼 다음 시간에는 이 새로 등장한 방법인 콘텐츠 기반 필터링에 대해 어떤 알고리즘으로 움직이는지, 장단점은 무엇인지, 어떻게 구현되는지에 대해서 알아보는 시간을 가져보도록 해요.
Made with